大學入學主要有三種入學管道:繁星推薦入學、個人申請入學(學測)與考試入學(指考),其中又以學測與指考為大宗。由於學測和指考的制度與考生族群不同,考生選擇學校的模式也就不同,因此較難直接比較兩個管道的考生選擇行為。
本系統針對學測與指考,透過統計與機器學習模型的運算來分析考生的選擇行為,提供學測的科系偏好分數,與指考的科系排名,依照類組與領域呈現。另外並提供依照學測資料所建構的科系競爭地圖,視覺化的呈現各科系的競爭強弱。競爭地圖假設兩個科系申請學生重複越多,則競爭越激烈。將這個成對的競爭關係,透過t-Distributed Stochastic Neighbor Embedding (t-SNE) 將結果投射到一個二維平面上,供大眾參考。
我們是誰?本網站是由臺灣大學資訊管理學系盧信銘副教授所帶領的大學專題成果,由B06級專題生林語萱架設,網站提供不同年度之學測申請入學偏好分數與指考排名、系所比對、競爭地圖以及2019年指考與學測排名比較分析。前一版本由B04級專題成員張芸瑄、曹哲瑜、黃敏、涂家瑋、黃獻霆架設,網站提供不同年度之學測申請入學偏好分數、系所資訊與網路圖。第一版(卡利基狂分析)由B02級專題成員謝宗翰、翁億宗、楊大為、李慶宏、何韋宏架設,為後續版本的雛型。
我們的排名方法?分為學測申請入學偏好分數排名與指考排名兩部分。
學測偏好分數排名
令某年度申請入學有系所數目 N、學生數目 T,則假設對所有考生有一組偏好分數\(a_1\)~\(a_n\),
使得某學生t選擇系所\(d_1\)的機率為 \(P_{t_1}= \frac{ e^{a_{d_1}} }{ e^{a_{d_1}}+e^{a_{d_2}}+ \cdots +e^{a_{d_k}} } \)。
為了估計這組偏好分數,我們使用 \( Cross Entropy Loss:\)\( \min -\sum_{i=1}^N y_i log P_{t_i} +\)\( \lambda \sum_{i=1}^N {a_i}^2 \)。
我們將申請入學各考生一階通過的系所作為考生可能的選擇集合,以考生最後錄取的科系為考生最後的選擇,據此資料用機器學習演算法最小化Cross Entropy Loss,計算各年度的偏好分數。
此分數不代表系所之間的優劣,而是考生的選擇及偏好。
關於此模型可參考:
指考排名
在大學聯考的時代,大眾一般依照各科系的最低錄取總分作為科系排名的依據。然而在指考的框架下,每個科系以選擇採計科目與各科加權的比重,因此公布的最低錄取總分無法直接比較。要解決這個問題,一個簡單的做法是把錄取總分除以權重總和,得到科目的加權平均分數。每個科系都這樣計算,就可以用這個加權平均分數排名。舉例而言,2018年交大電機的權重為國文x1.00,英文x1.50,數甲x2.00,物理x2.00,化學x1.00。錄取分數為640.75,因此加權平均分數為640.75 / 7.5 = 85.43。
這個做法主要的問題是各科系的平均分數可能經由不同權重調整,因此相互比較的可能有失公平。為了解決這個問題,我們發展了另一套調整權重的方式,可以讓我們更公平的比較各科系的最低錄取分數。這個調整方式可以在給定某科系考科權重與總分的前提下,估計某科系指定考科權重為1時的錄取總分。
這是一個條件期望值的估計問題。在假設各科目分數的分配為多變數常態的前提下,我們可以導出條件期望值的明解 (Closed-form Solution)。
具體而言,我們可以不失一般性的假設某年指考共有十考科。考生某甲的分數為\(X=[x_1,x_2,…,x_{10} ]^T\)。令某科系d的加權向量為\(a_d\),那考生某甲的總分為\(a_d^T X\)。我們想要知道的是,如果這個考生的加權向量不是\(a_d\),而是另一個加權向量\(a_0\),那這個新的總分\(a_0^T X\)應該是多少?
至於加權向量\(a_0的\)設值,我們將所有科系依據採計科目分為第一類組、第二類組與第三類組,將第一類組科系的國文、英文、數乙、歷史、地理、公民,第二類組科系的國文、英文、數甲、物理、化學,以及第三類組科系的國文、英文、數甲、物理、化學、生物科目權重設為1,其餘設為0。
我們假設這十個考科的分數服從多變數常態分配,均數向量為\(μ=[μ_1,μ_2,…,μ_{10} ]^T\),共變異數矩陣為Σ。那我們關心的就是條件機率分布\(P(a_0^T X│a_d^T X)\)的均數。
由於常態隨機變數的線性組合一樣也服從常態分布,因此我們知道\(a_0^T X\)與\(a_d^T X\)服從雙變數常態分布,均數為 \begin{bmatrix}a_0^T μ & a_d^T μ\end{bmatrix} 變異數矩陣為\begin{bmatrix}a_0^T Σa_0 & a_0^T Σa_d\\a_d^T Σa_0 & a_d^T Σa_d\end{bmatrix} 由\(P(a_0^T X│a_d^T X)=\frac{ p(a_0^T X, a_d^T X) }{ p(a_d^T X) }\),經過推導與化簡之後可以得到條件期望值的明解:
\(E[a_0^T X|a_d^T X]\)=\(a_0^T μ+\frac{a_0^T Σa_d}{a_d^T Σa_d } (a_d^T X-a_d^T μ)\) ......公式(*)
熟悉迴歸模型的人看到這個明解應該會很親切。
這裡雖然已經有公式(*),但卻無法直接應用。原因是各科分數的共變異數矩陣Σ未知。雖然大考中心有公佈詳細的各科分數的累積機率分配的資訊,卻沒有公佈科目分數的共變異數矩陣。因此如果要能使用這個公式,必須要先由公開資訊估計共變異數矩陣。
估計共變異數矩陣看似不可能的任務。然而,大學考試入學分發委員會有公佈每個考科組合總分的累積機率分配,例如數乙、歷史、地理的未加權總分人數累計表,以及數甲、物理、化學的未加權的總分人數累計表等。以2019年為例,扣除有採計音樂、體育、美術的組合之外,共有58個考科組合可以做為後續分析使用。我們的方法可以用這些考科組合資訊反推需要的共變異數矩陣。
這個做法的原理是利用隨機變數和的動差關係。為了方便說明,考慮某考科組合\(Y=X_1+X_2+X_3\),則
\(Var(Y)=\)\(Var(X_1)+Var(X_2)+Var(X_3)+\)\(2(σ_{1,2}+σ_{1,3}+σ_{2,3})\)
其中\(Var(Y)\)可以由未加權的各組合總分人數累計表算出,\(Var(X_1)\)、\(Var(X_2)\) 、\(Var(X_3)\)可由各科的人數累計表算出。如果我們將上式整理一下,可以得到
\(\frac{Var(Y) - Var(X_1) - Var(X_2) -Var(X_3)}{2}=\)\(σ_{1,2}+σ_{1,3}+σ_{2,3}\)
其中左邊是已知,右邊是未知的數值。將所有能找到的考科組合累計次數表依照上述的方法處理,就可以估計出未知的相關係數。
這個做法有幾個重要的細節。第一,有些相關係數實際上沒有資料可以估計,如物理與歷史。我們將這些相關係數直接設為0。第二,扣除直接設為0的相關係數之後,共有29個相關係數需要估計,而考科組合的數量一般大於需要估計的相關係數總數。以2019年為例,我們共有58個考科組合,但只需估計29個未知數。我們的解決方法也很直觀,就是找一組相關係數讓配適誤差最小。這件事可以很方便的使用現成的迴歸函數來執行。第三,有一些考科與組合因為缺考的關係,左尾有異常高的頻率,我們會先將這些離群值去除。
以這個方法求出的2019年指考科目的相關係數矩陣如下:
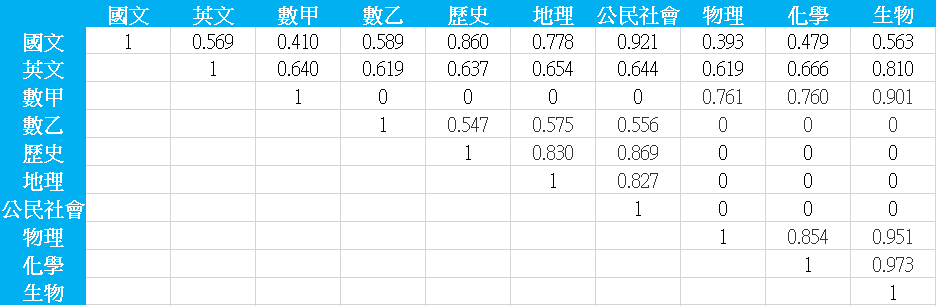
由於考科的相關係數沒有公開資料,我們並沒有辦法直接驗證這個做法的正確性,只能以直觀分析結果。所有考科相關係數最高的是生物與化學,相關係數高達0.973,接下來是生物與物理,有0.951。生物與數甲的相關係數也高達0.901。相關係數最低的組合是物理與國文,只有0.393。第二低的是國文與數甲,為0.410。化學與國文也是低檔(0.479)。估計出來的結果與直觀還算是相符合。
求得相關係數矩陣後就能反推共變異數矩陣並帶入公式(*),得到條件期望值的明解,也就是某科系考科指定權重為1時的估計錄取總分。每個系所都得到經過調整的錄取總分後,即可根據計算排名。
相關資料可參考:
我們如何比較排名?
由於學測和指考的制度與考生群眾不同,考生選擇學校與科系的模式也就不同,繼而影響各系所在兩個入學管道之下的排名有所差異。
本系統針對2019年的指考排名與學測偏好係數排名進行分析。此分析所用的指考排名為透過相關係數調整方法所計算出來的排名。首先將科系依據指考採計科目分成第一類組、第二類組、第三類組,每個類組再分別根據系所的所屬領域與學校分成群組。對於每一個類組的領域分群以及學校分群,我們用散佈圖視覺化的呈現各系所指考排名與學測偏好係數排名的分布關係,並且用迴歸模型分析群組的指考排名與學測排名差距均數。
領域分群用的是教育部提供的學門資料。而學校分群部分,第一類組與第二類組總共分成國立大學第一群、國立大學第二群、國立大學第三群、私立大學第一群、私立大學第二群、私立大學第三群六個群組,各群組所包含的學校如下(依學校代碼排序):
- 國立大學第一群:國立臺灣大學、國立成功大學、國立政治大學、國立清華大學、國立交通大學
- 國立大學第二群:國立臺灣師範大學、國立中興大學、國立中央大學、國立中山大學、國立中正大學、國立臺灣藝術大學、國立臺北大學
- 國立大學第三群:國立臺灣海洋大學、國立高雄師範大學、國立彰化師範大學、國立陽明大學、國立臺北藝術大學、國立臺中教育大學、國立臺北教育大學、國立臺南大學、國立東華大學、臺北市立大學、國立屏東大學、國立臺東大學、國立體育大學、國立暨南國際大學、國立臺灣體育運動大學、國立臺南藝術大學、國立嘉義大學、國立高雄大學、國立金門大學、國立聯合大學、國立宜蘭大學
- 私立大學第一群:東吳大學、高雄醫學大學、中原大學、東海大學、中國醫藥大學、淡江大學、逢甲大學、輔仁大學、中山醫學大學、長庚大學、元智大學、臺北醫學大學
- 私立大學第二群:大同大學、銘傳大學、世新大學、實踐大學、亞洲大學
- 私立大學第三群:中國文化大學、靜宜大學、大葉大學、中華大學、義守大學、長榮大學、南華大學、玄奘大學、真理大學、慈濟大學、開南大學、台灣首府大學、康寧大學、佛光大學、稻江科技暨管理學院、明道大學
第三類組總共分成四個群組,各群組所包含的學校如下(依學校代碼排序):
- 第一群: 國立臺灣大學、國立成功大學、高雄醫學大學、中國醫藥大學、國立陽明大學、中山醫學大學、長庚大學、慈濟大學、臺北醫學大學、馬偕醫學院
- 第二群: 國立清華大學、國立交通大學、國立臺灣師範大學、國立中央大學、國立中山大學、國立中正大學、國立臺灣海洋大學、國立高雄師範大學、國立彰化師範大學、國立臺南大學、國立東華大學、臺北市立大學、國立屏東大學、國立臺東大學、國立高雄大學、國立金門大學、國立宜蘭大學
- 第三群: 國立中興大學、國立嘉義大學
- 第四群: 東吳大學、中原大學、東海大學、輔仁大學、實踐大學、亞洲大學、中國文化大學、靜宜大學、大葉大學、中華大學、義守大學、長榮大學、南華大學
由於並非每個科系都同時以指考與學測作為入學管道,因此這個分析只將這兩個入學管道都有的科系納入。由於某些只有單一入學管道的科系被過濾掉了,因此以下分析所用的學測排名與指考排名,是將有納入分析的科系依照學測排名與指考排名重新計算的排序。
散佈圖
我們用散佈圖呈現各類組中科系的指考與學測排名的分布狀況,X軸是科系的指考排名,Y軸是科系的學測偏好係數排名。科系的顏色表示其所屬的領域或所屬的學校群組。散佈圖中特別列出了散佈在左上方與右下方的科系,也就是指考與學測排名相差較大的系所。
以第一類組來說,左上方列出的科系(指考排名相對於學測排名靠前)多屬於國立大學第三群,並且多屬於”商管法”領域,右下方列出的科系(學測排名相對於指考排名靠前)幾乎屬於私立大學第三群,領域較多元,主要屬於”商管法”、”藝術與人文”、”工程/營建”領域。
以第二類組來說,與第一類組的分布有相當差異,左上方的科系多屬於國立大學第二群,右下方的科系則幾乎都屬於國立大學第三群或私立大學第一群,而以領域分群來看則沒有明顯特徵,但右下方集中了一部分建築相關科系。
第三類組相較於第一類組與第二類組,比較沒有明顯特徵。
群組平均排名差分析
我們用迴歸模型針對群組的指考排名與學測排名平均差距進行分析。
以第一類組的學校分群為例,總共分成國立大學第一群、國立大學第二群、國立大學第三群、私立大學第一群、私立大學第二群、私立大學第三群六個群組,分別用 x1, x2, x3, x4, x5, x6六個變數來表示。我們採用Deviation Coding來對變數設值,例如x1將1分配給國立大學第一群、x2將1分配給國立大學第二群,以此類推,而私立大學第三群的變數值都分配為 -1,剩餘的其他值被分配為0,如下表:
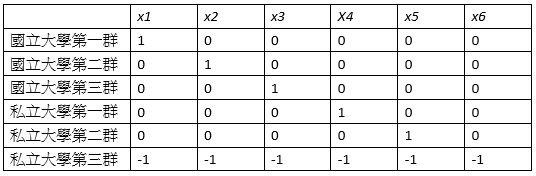
令\(yi\)為群組i中所有系所的指考排名減學測排名的均數,寫成迴歸式:
\(y_i=α+f_1 x_{i,1}+\)\(f_2 x_{i,2}+\)\(f_3 x_{i,3}+\)\(f_4 x_{i,4}+\)\(f_5 x_{i,5}+\)\(f_6 x_{i,6}+ϵ_i\)
為了方便討論,我們把i省略,式子變成
\(y= \)\(α+\)\(f_1 x_1+\)\(f_2 x_2+\)\(f_3 x_3+\)\(f_4 x_4+\)\(f_5 x_5+\)\(f_6 x_6+ϵ\)
對國立大學第一群來說,(x1, x2, x3, x4, x5, x6) = (1, 0, 0, 0, 0, 0),所以
\(y=α+f_1+ϵ\)
對這個式子取期望值,我們得到\(E[y│國立大學第一群]=α+f_1\)
同樣的作法,我們可以得到
\(E[y│國立大學第二群]=α+f_2\)
\(E[y│國立大學第三群]=α+f_3\)
\(E[y│私立大學第一群]=α+f_4\)
\(E[y│私立大學第二群]=α+f_5\)
\(E[y│私立大學第三群]= \)\( α-\)\(f_1-\)\(f_2-\)\(f_3-\)\(f_4-\)\(f_5\)
而條件期望值 \(E[y|國立大學第一群]\)其實就是把國立大學第一群的每筆資料(指考排名減學測排名)拿來算均數。如果把各組的均數加起來,\(E[y│國立大學第一群]\) + \(E[y│國立大學第二群]\) + \(E[y│國立大學第三群]\) + \(E[y│私立大學第一群]\) + \(E[y│私立大學第二群]\) + \(E[y│私立大學第三群]\) = \(α+\)\(f_1 + \)\(α+f_2 + \)\(α + f_3 + \)\( α + f_4 + \)\(α+ f_5 +\)\( α - \)\(f_1 - \)\(f_2 - \)\(f_3 - \)\(f_4 - \)\(f_5 = \)\( 6α\)
也就是說,迴歸截距項\(α\)是各群組均數的平均。此外,因為 \(E[y│國立大學第一群]=\)\((α+f_1\),所以\(f_1\)是國立大學第一群的均數跟各群組均數的平均的差值。
因此採用Deviation Coding能將給定群組的”指考排名減學測排名”均數跟各群組均數的平均值進行比較,而\(f_i\)即是群組i均數與各群組均數的平均的差值。所估計之\(f_i\)值若為正,表示該群組\(i\)的指考排名減學測排名之均數比整體均數大,我們可以理解為群組\(i\)的學測排名均數相對於指考排名均數較好;相反的,\(f_i\)值若為負,則表示群組\(i\)的指考排名減學測排名之均數比整體均數小,我們可以理解為群組\(i\)的指考排名均數比起學測排名均數較好。同理,\(f_i\)值正越多,表示群組\(i\)的學測排名均數相對於指考排名均數好越多;\(f_i\)值負越多,則表示群組\(i\)的指考排名均數相對於學測排名均數好越多。
迴歸分析之結果如下:
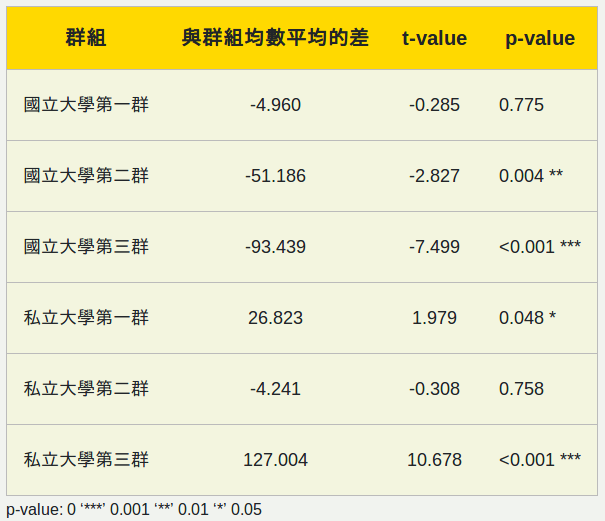
根據上表,可以分析2019年第一類組的指考排名與學測排名的關係: 從與均數平均差值部分來看,國立大學的三個群組以及私立大學第二群的值為負數,可以理解為這四個群組的指考排名均數相對於學測排名均數較好,而其中國立大學第二、三群達到顯著水準,因此我們有足夠信心去推斷,這兩個群組的指考排名均數是好於學測排名均數的,而國立大學第三群又較國立大學第二群明顯。而私立大學第一、三群的與均數平均差值為正數,且都達到顯著水準,因此我們有足夠信心去推斷,這兩個群組的學測排名均數好於指考排名均數,其中私立大學第三群尤為明顯。
總的來說,對於2019年第一類組,國立大學的指考排名均數有好於學測排名均數的現象,而私立大學除了第二群之外,有學測排名均數好於指考排均數名的現象。
我們使用的資料來源?
申請入學之偏好分數與競爭地圖使用 新鮮人查榜 與 交叉查榜網站 作為考生的選擇資料。
指考排名使用 大學考試入學分發委員會 提供之公開資料”各科成績人數累計總表”、”各組合成績人數累積總表”以及“各系組最低錄取分數及錄取人數一覽表”。
類組分類依據各系所指考的採計科目做分類,領域分類則使用 教育部提供之學門資料 。